라일리 상권 계산은 중심지 이론을 기반으로 상업 시설의 입지 및 상권 범위를 분석하는 데 활용되는 중요한 모델이다. 이는 컨버스 상권 계산식의 한계를 보완하며, 특정 지역에 새로운 상업 시설이 들어설 경우 기존 상권에 미치는 영향과 신설 상업 시설의 예상 상권 범위를 예측하는 데 유용하다. 이 글에서는 라일리 상권 계산의 기본 원리, 활용법, 그리고 실제 적용 사례를 심층적으로 분석한다.
1. 라일리 상권 계산의 이론적 배경
라일리 상권 계산은 윌리엄 라일리(William J. Reilly)가 1931년에 발표한 ‘소매 인력 법칙(Law of Retail Gravitation)’에 근거한다. 이 법칙은 두 도시 간의 상업적 인력은 각 도시의 인구에 비례하고, 두 도시 간 거리의 제곱에 반비례한다는 뉴턴의 만유인력 법칙을 상업 분야에 적용한 것이다. 즉, 인구가 많고 거리가 가까울수록 상업적 흡인력이 커진다고 본다.
라일리 상권 계산식은 이러한 소매 인력 법칙을 확장하여 특정 두 상업 중심지(도시 또는 상점) 사이에서 소비자들이 어느 쪽으로 이동할 것인지, 즉 ‘분기점(breaking point)’을 계산하는 데 초점을 맞춘다. 분기점은 두 상업 중심지의 상권이 나뉘는 지점을 의미하며, 이 지점에서는 두 중심지의 상업적 흡인력이 동일해진다.
2. 라일리 상권 계산식과 구성 요소
라일리 상권 계산식은 다음과 같다.
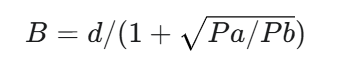
여기서 각 변수는 다음을 의미한다.
- B: 상권 분기점(Break-point)까지의 거리 (소규모 상권 중심지로부터의 거리)
- d: 두 상권 중심지 간의 총 거리
- Pa: 큰 상권 중심지의 인구 또는 상업적 규모 (예: 매출액, 점포 면적)
- Pb: 작은 상권 중심지의 인구 또는 상업적 규모 (예: 매출액, 점포 면적)
이 공식은 기본적으로 두 상권 중심지 중 더 큰 상권 중심지(인구 또는 규모가 큰 곳)의 영향력이 더 크다는 점을 반영한다. 따라서 분기점은 대개 작은 상권 중심지에서 더 가까운 곳에 형성된다.
3. 라일리 상권 계산의 활용
라일리 상권 계산은 다양한 비즈니스 상황에서 전략적으로 활용된다.
- 신규 점포 입지 선정: 경쟁 상권과의 관계를 고려하여 입지를 분석하고, 분기점을 기반으로 예상 고객 수를 추정한다.
- 기존 점포의 상권 재평가: 인구 변화나 경쟁 시설 등장에 따른 상권 이동을 예측해 전략을 조정한다.
- 마케팅 전략 수립: 분기점 주변 소비자를 대상으로 타겟 마케팅이나 프로모션을 기획한다.
- 도시 계획: 상업 시설의 적절한 배치와 지역 균형 발전을 위한 기초자료로 활용된다.
4. 라일리 상권 계산의 한계
- 교통 및 다중 상권 문제: 교통 인프라와 소비자의 다목적 방문 경로는 거리만으로 설명 불가
- 비합리적 소비자 행동: 브랜드 선호, 편의성, 분위기 등 비정량적 요인은 미반영
- 상업 시설의 특성 미반영: 편의점과 백화점의 상권 범위는 다름에도 구분하지 않음
- 동태적 변화 미반영: 상권은 시간에 따라 변하지만 공식은 정적인 분석만 가능
5. 보완 방안 및 통합 활용
- 컨버스 상권 계산과 병행: 라일리로 인력 계산, 컨버스로 지리적 경계 설정
- 허프 모델 결합: 소비자 선택 확률을 고려해 상권의 정밀도 향상
- GIS 기반 시각화: 데이터 기반 지도 분석으로 상권 구조를 직관적으로 파악
- 빅데이터 및 AI 도입: 소비 패턴, 이동 경로 분석을 통해 동태적 상권 변화 예측 가능
6. 결론
라일리 상권 계산은 상권 분석의 기초를 제공하는 강력한 도구이다. 하지만 이를 절대적 기준으로 삼기보다는, 현대 소비자의 복잡한 행동 양식과 시장 환경을 반영할 수 있도록 다양한 분석 기법 및 기술과 결합해 사용하는 것이 바람직하다. 결국 라일리 공식은 상권 전략 수립의 출발점이며, 이를 기반으로 한 통합적 접근이 성공적인 비즈니스를 위한 핵심이 된다.